Unleashed unicorn flying high – shunt mod for the NVIDIA GeForce RTX 3090 FE including Alphacool Eisblock GPX-N

As threatened last week, the Alphacool Eisblock GPX-N is not the only modification to my RTX 3090 Founders Edition. Today it’s about the shunt resistors, i.e. those with which the GPU measures how much power it is currently consuming and, if necessary, clocks itself down if NVIDIA’s limits of 350 or 400 W are reached. We also take another look at the assembly of the water block, because although the 19 ° C delta between water and GPU was not bad, it could admittedly be better.

Disclaimer

The following explains how the SMD components of the RTX 3090 Founders Edition graphics card can be physically modified in such a way that internal measuring devices of the GPU for determining the current intensity and power consumption are levered out. Correspondingly, the physical modification of the PCB will void the warranty. In addition, I am not a trained precision electronics technician and all of the procedures described have been learned myself. Therefore, this article should in no way be taken as a guide or recommendation, at most as an experiment or inspiration.

Shunt modding in theory

I don’t want to bore you with electrical engineering, some of you probably already know and the others were never interested in school, but a short outline of the theory should not be missing to understand what actually happens in the background and why the mod can work .

As the name suggests, a shunt or shunt resistor is a resistor that is installed in a circuit parallel to the actual consumer. This resistance has a fixed value, such as 5 mOhm in this case, and serves as a reference for the GPU to calculate the current strength and power. What the GPU also knows is the voltage that is present in front of the resistor, e.g. 12 V at the PCI-Express connections or in this case the NVIDIA 12-pin Microfit-Connector. This is simply measured in front of the shunt resistor.

The resistor now causes the applied voltage to drop, linearly with the current intensity flowing in the circuit. If the actual consumer to which the shunt is connected in parallel consumes more current, the voltage at the shunt also drops more sharply. The voltage is now measured again behind the shunt and the before-after results in a delta, the voltage drop. As this is linear and proportional to the current strength of the parallel consumer, as I said, it is now possible to directly deduce its power consumption.

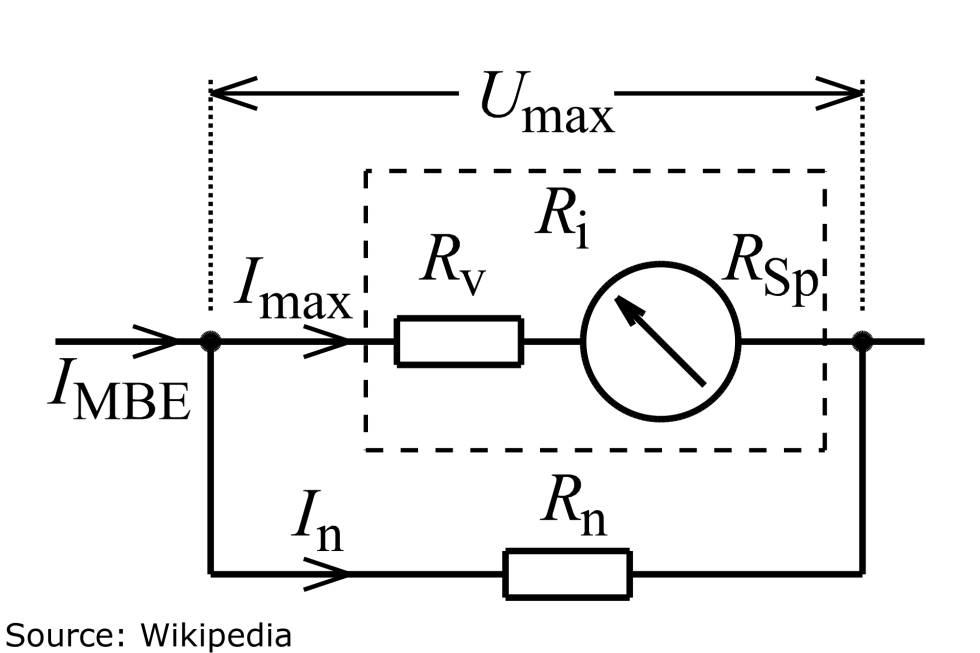
An example: There is exactly 12.0 V in front of the shunt, this has a resistance of 5 mOhm and the measured voltage after the shunt is 11.8 V. This results in a voltage drop of 0.2 V and thus together with the 5 mOhm, according to Ohm’s law, a current strength of 40 A (I = V / R). If this is now multiplied by the applied voltage of 12.0 V, the power consumption is 480 W (P = I * V). As I said, that was only an example, but it makes visible the few formulas and natural laws on which the whole thing is based.

And this is exactly where we can start now, because the GPU does not measure the resistance of the shunt, it just knows it, something NVIDIA burned into its memory. If we somehow manage to reduce the resistance, the voltage drop will also decrease, but the 5 mOhms are still used as the basis for the calculation and so the GPU thinks it uses less power and thus less power than in reality.

Another example: We use the data from the example above and know that 40 A of current is actually flowing. If we now reduce the shunt resistance to 2.5 mOhm and change the formula from above, this results in a voltage drop of only 0.1 V, i.e. 11.9 V measured after the shunt (V = I * R). This is reality, but the GPU still thinks the resistance is 5 mOhm and with the actual 0.1 V voltage drop it calculates a current of 20 A and thus a power consumption of 240 W.

As you can see, if you halve the shunt resistance, the circuit can allow itself to double the current and thus the power. Admittedly, this is a bit strange brain sport for laypeople, but once you understand these two formulas and have them roughly in your head, you can already develop a lot in electrical engineering. And of course there are enough calculators and resources on the Internet where you can look it up at any time, for example this one from Digi-Key